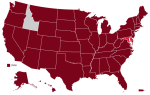
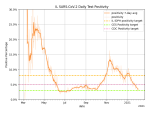
I usually tweet out Chicago-area Covid stats, but I thought I'd try something different today and post the information here on my blog. Most of the charts and maps are pulled from the wonderful Covid Act Now website. They take a lot of data and make it easy to understand.The national picture is looking extremely bleak, with the exception of Maryland, which is looking merely … [Read more...] about Covid Stats Dump – 2022-01-29
Science
N95 or Bust!
This tweet reminded me that it's probably time for an update to my series of posts on COVID-19 masking:Public health messaging about this has been terrible. The truth is that not all masks are created equally, and some masks are much better than others. I think public health authorities have been reluctant to say this out loud for a number of reasons, such as not wanting … [Read more...] about N95 or Bust!
Living with Covid is like being lost in the forest
A few weeks ago, I ran across an opinion column by Ben Shapiro titled "When does the COVID-19 panic end?" I keep thinking about it, and how much it pissed me off, so I decided I might as well get it out of my system by writing about it.Two weeks to slow the spread.That was the original rationale for the lockdowns, masking and social distancing: Prevent transmission of … [Read more...] about Living with Covid is like being lost in the forest
Some Useful Sources of COVID-19 Data
Like many people, I've spend the past year trying to understand what's happening with the pandemic, and I thought it might be useful to share some of my favorite websites for data on COVID-19 in the United States.CovidActNowIf you want a one-stop snapshot of how the pandemic is going, start at CovidActNow. They don't have a lot of fancy data tables and charts. Instead, … [Read more...] about Some Useful Sources of COVID-19 Data
The Windypundit Immunity Model
Some of you may know that I tweet out COVID-19 statistics and commentary once a week. One of my goals with this blog -- and by extension, my Twitter stream -- is that no one should be stupider for having read it. Since I'm not a professional epidemiologist, I try not to get too far outside the data in reaching for things to say. In particular, I have avoided the temptation of … [Read more...] about The Windypundit Immunity Model