As I explained in the first post of this series, I’m trying to build a computer model of certain aspects of the criminal justice system. This week, it’s not going well.
My goal is to build a model of how our justice system handles plea bargains, with an eye toward understanding (1) why a system built around the highly formalized decision-making mechanism of the trial doesn’t actually have many trials, and (2) what we can do about it. As I am neither a professional systems modeler nor a lawyer, this is mostly intended as a learning experience.
I plan to eventually give the model a bunch of parameters such as time spent waiting for trial, case quality, sentencing regime, defendant risk tolerance. If I do a good job building the model, then I should be able to find a set of parameters that make the model produce results that look like our criminal justice system: Lots of plea bargains, very few trials, etc. Then I can experiment with ideas for reform by tweaking the model parameters to see how the model responds.
I’m taking an iterative approach to building the model, starting with a skeleton that has some of the major moving parts of the criminal legal process, and then elaborating on parts of the model to flesh it out into something more realistic.
The most recent model is very simple: There’s only one crime, people are arrested at a fixed rate, they wait in jail for a fixed time, and then they have a trial, after which they may go to jail for a fixed period. I suspect my lawyer readers will be annoyed to learn that the entire trial — the core of their profession — is modeled as a single draw from a random distribution to get the verdict. Plea bargaining, my whole reason for doing this, isn’t even in the model yet.
It’s that last problem that I tried to fix. I’m trying to add a plea bargaining phase somewhere between arrest and trial, and I’d like to tell you about it. This story will not end well.
I started by thinking about the basic decision the defendant has to make during plea bargaining: Take the prosecution’s offer or reject it and go to trial. I think there are two main question to address: What does the defendant know? And what does the defendant prefer?
I’m assuming the defendant has knowledge of a few basic things:
- The amount of time in the plea offer from the prosecution.
- The possible outcomes of the trial, consisting of:
- The probability of being found guilty.
- The sentence they will serve if found guilty.
Here you see more of my assumptions: Everybody has the same information, and it’s correct information as far as it goes. Note that I’m not saying anyone knows how the trial will turn out ahead of time — I’m modeling it as a draw from a random variable — but I am assuming that both the prosecutor and defense know what that probability is, and that both can use it to make decisions.
When thinking about a random event, it’s helpful to consider the expected outcome, which is calculated as the sum of the value of each outcome times the probability of that outcome. If you buy a raffle ticket which has a 1-in-10 chance of winning $50, we can calculate the expected value of your ticket as follows: Your 1-in-10 chance is a way of saying p = 0.1 for winning, so we multiply that by the payoff, $50, and get $5. Your 9-in-10 chance of losing has p = 0.9, but you get nothing for that, so the value of losing goes to $0. Add up the expected value for all possible outcomes (5 + 0), and you get the expected value of your ticket: $5.
Similarly, if the defendant knows he will be found guilty half the time (p = 0.5), and he knows the sentence is 10 years, he can calculate the expected sentence as (0.5 x 10 =) 5 years. Once he receives the prosecutor’s plea offer, he knows everything he needs to know (under this model) to make a decision.
The key issue controlling the defendant’s decision is then his attitude toward the risk of going to trial. If the prosecutor’s plea offer is 5 years in jail — exactly equal to the expected sentence calculated above, then you could argue that the defendant should be indifferent to the choice between taking the offer or going to trial, since the expected sentence is 5 years either way.
The problem with that approach is that it ignores risk, and people don’t usually ignore risk. All other things being equal, people usually prefer to reduce their risk. There is a massive amount of evidence for this, including the existence of the entire insurance industry, where customers pay fixed premiums to avoid the risk of having to suffer losses. If this risk aversion extends to plea bargaining decisions, a defendant will choose a certain sentence of 5 years in jail over a 50% chance of spending 10 years in jail, even thought the latter also includes a 50% chance of going free.
But if the defendant prefers a 5-year plea over a trial with a 50% risk of a 10-year sentence, what happens if the prosecutor makes an offer of 5 years and 1 month instead? Well, the insurance industry is pretty profitable, which means that people are paying more in premiums than their insurance companies are paying out to cover losses, which means that (on average) customers lose money when they buy insurance. So I think it’s very likely that a defendant will agree to lose an extra month of life in prison to protect against the risk of losing an extra five years of life in prison. If criminal defendants are risk averse, they would be willing to accept a plea bargain for more time than the mathematically expected sentence.
I am modeling this risk aversion by calculating an adjustment to the probability of guilt that represented how that probability would feel to a risk-averse defendant. E.g. a 50% (p = 0.5) probability of guilt with a 10-year sentence has a mathematically expected sentence of 5 years, but to a risk averse defendant, even a 6-year sentence might be preferable to a 50% risk of a 10 year sentence.
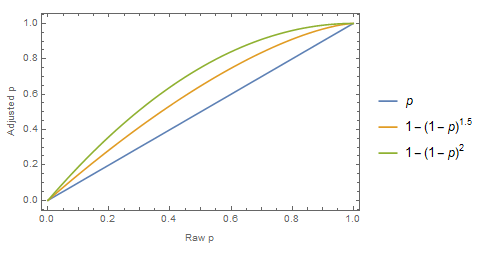
I decided to calculated the adjusted risk-averse factor by calculating an expected probability of an acquittal as 1 – p, then raising it to a power specified as a model parameter, and then converting back to a probability of guilt by subtracting it from 1 again. E.g.
1 – (1 – p)a
where
p is probability of guilt
a is the risk aversion model parameter
I picked this method of modeling risk aversion because (1) I vaguely remember reading an article about risk aversion that modeled it like this, (2) it has the nice property that p = 0 and p = 1 both map to themselves, so it stays in range, and (3) I like the look of the curve. Here, for example, are the curves with a set to 1, 1.5, and 2 for comparison. Remember a = 1 means no risk aversion.
Now that I had a simple model for defendant choice, it was time to model the prosecution.
One of the fundamental differences between defendants and prosecutors, at least for purposes of my model, is that defendants are individuals who seek their own advantage in a single criminal case, whereas prosecutors work together across hundreds or thousands of trials to achieve a common organizational goal. So while I feel reasonably comfortable in assuming for purposes of the model that most criminal defendants will try to minimize their risk-adjusted prison sentence, I’m not nearly as confident in figuring out what exactly prosecutors are trying to achieve.
To keep the model simple, I’m going to assume that prosecutors want the opposite of what defendants want. That is, if defendants want to minimize the risk-adjusted sentence they expect, prosecutors want to maximize the aggregate expected prison sentence across all defendants.
You’ll notice I didn’t say the prosecution goal was risk-adjusted. That’s because if defendants are like insurance buyers, prosecutors are like insurance companies. For an individual home owner, the loss of their house to fire would be financially devastating without an insurance policy. But to the company that issued the policy, it’s just business. They issued policies for tens or hundreds of thousands of homes, and they are well aware that a bunch of them are going to burn down every year. Meanwhile, they will be collecting premiums on all of them, and very nearly all of them will survive through the year with no loss whatsoever. In investment terms, insurance companies are “diversifying away” the risk.
Prosecutors can do something similar. Using the example from above, a defendant going to trial against a 50% chance of a 10-year sentence has a mathematically expected sentence of 5 years, but he’s not going to serve 5 years. He’s going to serve either zero or 10 years. On the other hand, a prosecution team that deals with 100 of these trials will have a mathematically expected sentence of 5 years per case, which adds up to a aggregate expected sentence across all cases of 500 prisoner-years. And they’re actually going to get about 500 prisoner-years, which is 50% of the theoretical maximum of 1000 prisoner-years. In other words, in the long run, the prosecutor can earn the expected sentence on average.
Furthermore, defendants can only accept or reject the deal that the prosecutor offers them, but the prosecutor’s office can offer whatever deal they want, including dismissal or no deal, to all of the defendants. This means it’s ultimately the prosecutor who gets to decide which defendants get plea bargains.
However, they have to do that within a resource constraint: There’s a limit on the number of trials the justice system can support in any given time period (at least for the short term). So if 100 cases enter the system, there might only be enough capacity in the system for 30 full trials. For the system to keep functioning, the remaining 70 cases will have to be disposed of with a plea bargain.
But how do they choose which defendants get plea deals and which ones go to trial? Well, consider this batch of defendants:
| ID | Probability of Guilt | Sentence if Convicted | Mathematically Expected Sentence | Risk Aversion Adjusted Probability of Guilt | Acceptable Plea | Difference Between Acceptable Plea and Expected Sentence |
| A | 0% | 10 | 0.000 | 0.000 | 0.000 | 0.000 |
| B | 10% | 10 | 1.000 | 0.178 | 1.778 | 0.778 |
| C | 20% | 10 | 2.000 | 0.299 | 2.991 | 0.991 |
| D | 30% | 10 | 3.000 | 0.405 | 4.054 | 1.054 |
| E | 40% | 10 | 4.000 | 0.503 | 5.030 | 1.030 |
| F | 50% | 10 | 5.000 | 0.595 | 5.946 | 0.946 |
| G | 60% | 10 | 6.000 | 0.682 | 6.817 | 0.817 |
| H | 70% | 10 | 7.000 | 0.765 | 7.653 | 0.653 |
| I | 80% | 10 | 8.000 | 0.846 | 8.459 | 0.459 |
| J | 90% | 10 | 9.000 | 0.924 | 9.240 | 0.240 |
| K | 100% | 10 | 10.000 | 1.000 | 10.000 | 0.000 |
The first three colums show the probability of being found guilty, the fixed 10-year sentence, and the resulting mathematically expected sentence. The fourth column shows the probability of guilt adjusted for risk aversion (using an exponent of 3/4), and then the plea that the defendant would be willing to accept based on that risk adjustment. Finally, the last column shows the difference between the plea and the mathematically expected sentence. I.e. the premium in prison time that the defendant is willing to pay to reduce the risk of a 10-year sentence.
At this point, the prosecution plea bargaining strategy seemed obvious to me: If the goal is to maximize aggregate prison time, then the prosecution can maximize total prison time by offering plea deals to those defendants willing to accept the most additional prison time beyond beyond the mathematically expected sentence. Thus, if they only have resources for 3 trials for the defendants above, they should dismiss the unwinnable case A, plea out B through H, and go to trial on defendants I, J, and K.
That’s when I realized I had screwed up: If the prosecution is trying to maximize aggregate prison time, and if defendants will agree to more than the mathematically expected sentence because they are risk averse, then why would the prosecution ever go to trial on any case? By the assumptions I had made, they could always get more prison time with a plea offer. And yet…trials happen.
There’s a mistake in here somewhere. Possibly more than one. Either I’ve oversimplified my model, or else it’s flat-out wrong. Or both. A few possibilities spring immediately to mind:
- Maybe I was wrong to assume both sides see the same probability of guilt. The sides in each case could have randomly different views of the quality of any given case. For all I know, all trials occur because the prosecution thinks it will be easier to prove guilt than the defense does.
- Defendants may be risk-preferring instead of risk averse. Conventional wisdom is that criminals are more willing to tolerate risk than law abiding people. Or risk-preferring people, criminal or not, may be more likely to attract police attention.
- Prosecutors may be optimizing for something other than aggregate prison sentence, such as conviction rate. Or prison times may combine in a non-linear manner: E.g. five 20-year sentences may be better for a prosecutor’s career than twenty 5-year sentences.
- Maybe collateral (non-prison) effects of a conviction affect defendants’ decisions in ways that matter. E.g. If any conviction, including by plea bargain, could result in deportation, defendants might grasp at even small chances at trial.
- I may need a more complex model of the trial outcome than just a probability of conviction. Maybe there are important phases or types of cases. Or maybe one side has more information and can consistently make better choices.
- Maybe I need to account for interactions between cases in the prosecutors’ decision making. E.g. taking 5 aggravated battery cases to trial may use up resources that could be used on a murder case, which could affect how they make plea bargains.
Time to go back to the drawing board. At the very least, I’ve got some thinking to do. And maybe it’s time for me to actually read something written by people who study this stuff.
Leave a ReplyCancel reply