One of the limitations of the Model Justice 1.0 model is that every defendant has the exact same probability of being found guilty at trial. That’s unrealistic, and it’s unrealistic in a way that will matter: The estimation of the probability of a conviction at trial has got to be one of the most important factors in whether a prosecutor decides to offer a plea deal and whether a defendant decides to accept one.
What I want to do in the simulation is to assign a probability p to every defendant who enters the model. This will represent the probability of conviction if the case goes to trial. I.e. if p = 0.25 then there is a 25% chance the defendant will be found guilty by the Verdict action when it runs. If p = 0, there’s no chance of a conviction, and if p = 1, there’s no chance of an acquittal. But before I can do that, I need to answer an important question: How should those probabilities be distributed? Or to put it in the language of the problem domain: How does the quality of the criminal cases vary?
The easiest approach is to assume a uniform distribution. That is, to assume that all possible values of p from 0 to 1 are equally likely, so that a 100-bin histogram of the probability of guilt for 100,000 cases would look something like this, with the values spread out more-or-less equally over all the quality levels.
That doesn’t seem realistic to me. I mean, does it seem right that they would bring just as many cases that will succeed 5% of the time as will succeed 50% of the time? I just don’t believe that the prosecution would bring exactly as many cases at each possible probability of success.
This is where it would be great to use research by professional criminologists, or get advice from people with a lot of experience in the criminal justice system, who might be able to advise me on the quality mix of criminal cases. Alternatively, it would be nice to pull these numbers from a sophisticated model of how the police and prosecutors’ offices build cases. Since I don’t have access to either of those right now, I’m just going to wing it.
I’m going to assume that building a case that will persuade a jury involves trying to achieve a whole bunch of smaller subgoals, and that each of these goals would improve the case in a way that pushes the jury toward a guilty vote — the more goals accomplished, the likely the jury is to convict. If we assume that the prosecutor and police officers have a roughly equal probability of accomplishing each of these goals, then the number of goals accomplished will conform to what is known as a binomial distribution.
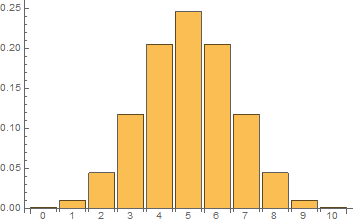
A good example of a binomial distribution is the probabilities of various outcomes when we flip ten coins and count how many turn up heads. Since each coin has two possible values, and there are 10 coins, there are 210 = 1024 possible outcomes. Of those outcomes, the extreme cases of all heads or all tails can each only occur one way:
HHHHHHHHHH TTTTTTTTTT
So the probability of either of those cases is 1/1024 ≈ 0.000977.
There are 10 possible ways of having one coin come up heads, one for each coin:
HTTTTTTTTT THTTTTTTTT TTHTTTTTTT TTTHTTTTTT TTTTHTTTTT TTTTTHTTTT TTTTTTHTTT TTTTTTTHTT TTTTTTTTHT TTTTTTTTTH
So the probability of exactly one head in a set of flips is 10/1024 ≈ 0.00977. That’s also the probability of exactly one tail in the set of flips.
Now it gets more complicated. For two coins to come up heads, there are a bunch of ways it can happen. We already know there are 10 ways to get 1 head. So assuming we’ve got one head, there are 9 remaining coins, and any one of those can also come up heads. However, that leads to each combination appearing twice. E.g. we can start with TTTHTTTTTT and then pick anther coin to get TTTHTTTHTT. However, that gives the same result as if we had started with TTTTTTTHTT and picked another coin to get TTTHTTTHTT. In other words, the two possible ways of choosing two heads result in identical sets of flips, so we have to divide by 2. That means the number of ways of getting exactly 2 heads is (10 x 9) / 2 = 45 which occurs with a probabiliy of 45/1024 ≈ 0.0439.
There are 10 x 9 x 8 ways to get to 3 heads, divided by 3 x 2 ways to arrange 3 heads identically, leaving 120 possible ways to get exactly 3 heads or 3 tails, with a probability of 0.117. By similar logic, 4 heads or 4 tails come up 210 ways with a probability of 0.205, and 5 of each comes up 252 ways with a probability of 0.246
If we plot the possibility of each possible number of heads, the probabilities look like this:
For Model Justice 1.1, I’m going to be assuming that the quality of cases charged against defendants assume a similar profile. I don’t know how many factors go into building a criminal case, but I assume it’s a lot more than 10. And since I’m just picking a distribution rather than modeling each of the factors, I don’t really have to care. That means that instead of using a binomial distribution, which depends on a fixed number of factors (you can’t flip 8.7 coins), I’m going to use a continuous approximation to the binomial distribution called the normal distribution, which looks something like this:
This is, I must admit, something of a cop-out. The normal distribution is probably the most common distribution ever, at least when discussing real-world phenomena. (Uniform distributions are common in games and gambling.) In fact, scientists often assume data points are normally distributed even when they really aren’t. It’s one of the sins of statistics, usually committed because there are so many more statistical tools available if you can just assume normality.
However, when dealing with data taken from the real world, there are solid statistical reasons for believing that the normal distribution may be close enough. The real world is often messy, with lots of different effects contributing to the thing you are trying to measure. And when a measurement is influenced by lots of small random variables, each of which can nudge it slightly higher or lower, it turns out that the result often does look a lot like a normal distribution.
This can be illustrated with something called a Galton board. That’s a slanted board with pins sticking up out of it in a regular pattern of offset rows. You drop balls into it at the top, and they trickle down. Each time they hit a pin, they can roll off to the left or right, at which point they will hit a pin from the row below, again rolling off to the left or right, and so on. At the bottom of the board, right below the last row of pins, there’s a set of vertical slots to catch and stack the balls. The height of the stack will tell you how many balls ended up there, and if you dump enough balls into the board, the stacks will follow (more or less) a normal curve.
Here’s a decent video with some explanation (skipping the Galton bio at the beginning):
(You can buy the Galton board used in the video here.)
So that’s my justification for using a normal distribution. I can imagine of a number of reasons why the quality of actual criminal cases wouldn’t follow a normal curve but, at least for now, it’s good enough.
I do need to make some adjustments to fit the model. For one thing, the allowable values for a defendants probability of guilt are from 0 to 1, so I might want to drop the normal curve right in the middle of it, something like this:
There are a couple of problems with that idea.
First of all, the normal distribution is a mathematical construct, so despite the nice appearance here, the left and right tails actually extend out to infinity. So what does it mean if we pick a random value out of the normal curve and the probability of guilt is 3.5? My thinking is that the normal curve doesn’t really represent the probability of guilt. Rather, it’s a crude representation of the quality of the case. So if we get values that are greater than 1, it means the case is more than good enough to guarantee (with p = 1) a conviction. Similarly, a case quality less than 0 means there is no way (p = 0) it could lead to a conviction. So if I get a value outside the range 0 to 1, I’ll snap it to 0 or 1.
The second problem is that there’s no reason to believe the average probability of guilt is exactly 0.5. As I said, the normal distribution actually represents the quality of the case, and it would be quite a coincidence if the average case quality just happened to be exactly good enough to produce a perfect split between guilty and not guilty verdicts. It’s likely that strong cases are more work to put together than week cases, so there will be a tendency to produce a lot of weak cases:
Then again, it’s possible that prosecutors avoid charging extremely weak cases that they don’t think they can win, leaving only the strong cases:
The third problem is that cases may deviate from normality in important ways. For example, the practice of discarding bad cases may lead to a different shape of the left-hand side of the distribution curve. Or maybe there’s always a small chance of a not-guilty verdict, from jury excursions or random black swan events, so that even the best cases can sometimes lose. I have no idea, so I’m going to ignore these possibilities for now. (I may add something in later.)
Incorporating this into the model is pretty straightforward, and you can follow along on the new Model Justice 1.1 model.
The shape of a normal distribution curve is described with two values:
- Mean: The average value. Or the value right in the middle of the curve at the highest point. (One of the handy properties of normal distributions is that the mean, median, and mode are all the same.)
- Standard Deviation: This is basically a measurement of how wide the curve is. The greater the standard deviation, the more the curve stretches out to the left and right.
I’ve replaced the Probability of Guilt slider, and the underlying variable, with Guilt Mean and Guilt Standard Deviation sliders that control the shape of the normal distribution. The values shown will cause this model to produce the same ProbGuilty values as version 1.0:
I also modified the code in the Arrest action to generate a random value from the normal distribution. If the value is outside the range [0,1], it will be snapped to the nearest bound. I.e. Values greater than 1 will be snapped to 1 and negative values will be snapped to 0 so they are valid probabilities. Unfortunately, Insight Maker doesn’t give me any way to show the shape of the generated curve. If you want to get some idea what the curves look like, you can use an online normal curve generator, like this one.
(I’ve also added an ID generator that slaps an ID number on each defendant agent, and I’ve added a global Stats object that collects some internal data that I use for debugging.)
Sadly, after all this discussion, the results from the new model are not noticeably different from the results from the old model. It was generating random guilt probabilities around a specified mean, now the new model is generating random guilt probabilities around a mean that is itself randomly generated around a mean. That tends to look like the same thing.
Nevertheless, these changes are a step toward modeling plea bargaining, because they will keep all defendants from making the same decisions.
Leave a ReplyCancel reply